NPTEL Introduction to Machine Learning Assignment 2 Answers 2023:- In this post, We have provided answers of NPTEL Introduction to Machine Learning Assignment 2. We provided answers here only for reference. Plz, do your assignment at your own knowledge.
NPTEL Introduction To Machine Learning Week 2 Assignment Answer 2023
1. The parameters obtained in linear regression
- can take any value in the real space
- are strictly integers
- always lie in the range [0,1]
- can take only non-zero values
Answer :- a. can take any value in the real space
2. Suppose that we have N independent variables (X1,X2,…Xn) and the dependent variable is Y . Now imagine that you are applying linear regression by fitting the best fit line using the least square error on this data. You found that the correlation coefficient for one of its variables (Say X1) with Y is -0.005.
- Regressing Yon X1 mostly does not explain away Y .
- Regressing Y on X1 explains away Y .
- The given data is insufficient to determine if regressing Yon X1 explains away Y or not.
Answer :- b. Regressing Yon X1 mostly does not explain away Y .
3. Which of the following is a limitation of subset selection methods in regression?
- They tend to produce biased estimates of the regression coefficients.
- They cannot handle datasets with missing values.
- They are computationally expensive for large datasets.
- They assume a linear relationship between the independent and dependent variables.
- They are not suitable for datasets with categorical predictors.
Answer :- c. They are computationally expensive for large datasets.
4. The relation between studying time (in hours) and grade on the final examination (0-100) in a random sample of students in the Introduction to Machine Learning Class was found to be:Grade = 30.5 + 15.2 (h)
How will a student’s grade be affected if she studies for four hours?
- It will go down by 30.4 points.
- It will go down by 30.4 points.
- It will go up by 60.8 points.
- The grade will remain unchanged.
- It cannot be determined from the information given
Answer :- c. It will go up by 60.8 points.
5. Which of the statements is/are True?
- Ridge has sparsity constraint, and it will drive coefficients with low values to 0.
- Lasso has a closed form solution for the optimization problem, but this is not the case for Ridge.
- Ridge regression does not reduce the number of variables since it never leads a coefficient to zero but only minimizes it.
- If there are two or more highly collinear variables, Lasso will select one of them randomly
Answer :- c. Ridge regression does not reduce the number of variables since it never leads a coefficient to zero but only minimizes it. d. If there are two or more highly collinear variables, Lasso will select one of them randomly
6. Find the mean of squared error for the given predictions:
Hint: Find the squared error for each prediction and take the mean of that.
- 1
- 2
- 1.5
- 0
Answer :- a. 1
7. Consider the following statements:
Statement A: In Forward stepwise selection, in each step, that variable is chosen which has the maximum correlation with the residual, then the residual is regressed on that variable, and it is added to the predictor.
Statement B: In Forward stagewise selection, the variables are added one by one to the previously selected variables to produce the best fit till then
- Both the statements are True.
- Statement A is True, and Statement B is False
- Statement A is False and Statement B is True
- Both the statements are False.
Answer :- a. Both the statements are True.
8. The linear regression model y=a0+a1x1+a2x2+…….+apxp is to be fitted to a set of N training data points having p attributes each. Let X be N×(p+1) vectors of input values (augmented by 1‘s), Y be N×1 vector of target values, and θθ be (p+1)×1 vector of parameter values (a0,a1,a2,…,ap. If the sum squared error is minimized for obtaining the optimal regression model, which of the following equation holds?
Answer :- d. XTXθ=XTY
9. Which of the following statements is true regarding Partial Least Squares (PLS) regression?
- PLS is a dimensionality reduction technique that maximizes the covariance between the predictors and the dependent variable.
- PLS is only applicable when there is no multicollinearity among the independent variables.
- PLS can handle situations where the number of predictors is larger than the number of observations.
- PLS estimates the regression coefficients by minimizing the residual sum of squares.
- PLS is based on the assumption of normally distributed residuals.
- All of the above.
- None of the above.
Answer :- a
10. Which of the following statements about principal components in Principal Component Regression (PCR) is true?
- Principal components are calculated based on the correlation matrix of the original predictors.
- The first principal component explains the largest proportion of the variation in the dependent variable.
- Principal components are linear combinations of the original predictors that are uncorrelated with each other.
- PCR selects the principal components with the highest p-values for inclusion in the regression model.
- PCR always results in a lower model complexity compared to ordinary least squares regression.
Answer :- c. Principal components are linear combinations of the original predictors that are uncorrelated with each other.
| Course Name | Introduction To Machine Learning |
| Category | NPTEL Assignment Answer |
| Home | Click Here |
| Join Us on Telegram | Click Here |
NPTEL Introduction To Machine Learning Week 2 Assignment Answer 2023
1. The parameters obtained in linear regression
- can take any value in the real space
- are strictly integers
- always lie in the range [0,1]
- can take only non-zero values
Answer :- Click Here
2. Suppose that we have N independent variables (X1,X2,…Xn) and the dependent variable is Y . Now imagine that you are applying linear regression by fitting the best fit line using the least square error on this data. You found that the correlation coefficient for one of its variables (Say X1) with Y is -0.005.
- Regressing Yon X1 mostly does not explain away Y .
- Regressing Y on X1 explains away Y .
- The given data is insufficient to determine if regressing Yon X1 explains away Y or not.
Answer :- Click Here
3. Which of the following is a limitation of subset selection methods in regression?
- They tend to produce biased estimates of the regression coefficients.
- They cannot handle datasets with missing values.
- They are computationally expensive for large datasets.
- They assume a linear relationship between the independent and dependent variables.
- They are not suitable for datasets with categorical predictors.
Answer :- Click Here
4. The relation between studying time (in hours) and grade on the final examination (0-100) in a random sample of students in the Introduction to Machine Learning Class was found to be:Grade = 30.5 + 15.2 (h)
How will a student’s grade be affected if she studies for four hours?
- It will go down by 30.4 points.
- It will go down by 30.4 points.
- It will go up by 60.8 points.
- The grade will remain unchanged.
- It cannot be determined from the information given
Answer :- Click Here
5. Which of the statements is/are True?
- Ridge has sparsity constraint, and it will drive coefficients with low values to 0.
- Lasso has a closed form solution for the optimization problem, but this is not the case for Ridge.
- Ridge regression does not reduce the number of variables since it never leads a coefficient to zero but only minimizes it.
- If there are two or more highly collinear variables, Lasso will select one of them randomly
Answer :- Click Here
6. Find the mean of squared error for the given predictions:
Hint: Find the squared error for each prediction and take the mean of that.
- 1
- 2
- 1.5
- 0
Answer :-
7. Consider the following statements:
Statement A: In Forward stepwise selection, in each step, that variable is chosen which has the maximum correlation with the residual, then the residual is regressed on that variable, and it is added to the predictor.
Statement B: In Forward stagewise selection, the variables are added one by one to the previously selected variables to produce the best fit till then
- Both the statements are True.
- Statement A is True, and Statement B is False
- Statement A is False and Statement B is True
- Both the statements are False.
Answer :- Click Here
8. The linear regression model y=a0+a1x1+a2x2+…….+apxp is to be fitted to a set of N training data points having p attributes each. Let X be N×(p+1) vectors of input values (augmented by 1‘s), Y be N×1 vector of target values, and θθ be (p+1)×1 vector of parameter values (a0,a1,a2,…,ap. If the sum squared error is minimized for obtaining the optimal regression model, which of the following equation holds?
Answer :- Click Here
9. Which of the following statements is true regarding Partial Least Squares (PLS) regression?
- PLS is a dimensionality reduction technique that maximizes the covariance between the predictors and the dependent variable.
- PLS is only applicable when there is no multicollinearity among the independent variables.
- PLS can handle situations where the number of predictors is larger than the number of observations.
- PLS estimates the regression coefficients by minimizing the residual sum of squares.
- PLS is based on the assumption of normally distributed residuals.
- All of the above.
- None of the above.
Answer :-
10. Which of the following statements about principal components in Principal Component Regression (PCR) is true?
- Principal components are calculated based on the correlation matrix of the original predictors.
- The first principal component explains the largest proportion of the variation in the dependent variable.
- Principal components are linear combinations of the original predictors that are uncorrelated with each other.
- PCR selects the principal components with the highest p-values for inclusion in the regression model.
- PCR always results in a lower model complexity compared to ordinary least squares regression.
Answer :- Click Here
| Course Name | Introduction To Machine Learning |
| Category | NPTEL Assignment Answer |
| Home | Click Here |
| Join Us on Telegram | Click Here |
NPTEL Introduction to Machine Learning Assignment 2 Answers 2022 [July-Dec]
Q1. The parameters obtained in linear regression
a. can take any value in the real space
b. are strictly integers
c. always lie in the range [0,1]
d. can take only non-zero values
Answer:- a
2. Suppose that we have NN independent variables (X1,X2,…XnX1,X2,…Xn) and the dependent variable is YY . Now imagine that you are applying linear regression by fitting the best fit line using the least square error on this data. You found that the correlation coefficient for one of its variables (Say X1X1) with YY is -0.005.
a. Regressing Y on X1 mostly does not explain away Y.
b. Regressing Y on X1 explains away Y.
c. The given data is insufficient to determine if regressing Y on X1 explains away Y or not.
Answer:- a
Answers will be Uploaded Shortly and it will be Notified on Telegram, So JOIN NOW
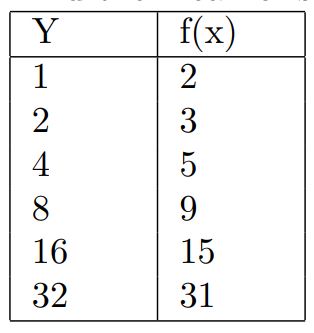
3. Consider the following five training examples

We want to learn a function f(x) of the form f(x)=ax+b which is parameterised by (a,b).Using mean squared error as the loss function, which of the following parameters would you use to model this function to get a solution with the minimum loss?- (4, 3)
- (1, 4)
- (4, 1)
- (3, 4)
Answer:- b
4. The relation between studying time (in hours) and grade on the final examination (0-100) in a random sample of students in the Introduction to Machine Learning Class was found to be:
Grade = 30.5 + 15.2 (h)
How will a student’s grade be affected if she studies for four hours?
a. It will go down by 30.4 points.
b. It will go down by 30.4 points.
c. It will go up by 60.8 points.
d. The grade will remain unchanged.
e. It cannot be determined from the information given
Answer:- c
5. Which of the statements is/are True?
a. Ridge has sparsity constraint, and it will drive coefficients with low values to 0.
b. Lasso has a closed form solution for the optimization problem, but this is not the case for Ridge.
c. Ridge regression does not reduce the number of variables since it never leads a coefficient to zero but only minimizes it.
d. If there are two or more highly collinear variables, Lasso will select one of them randomly.
Answer:- c, d
6. Consider the following statements:
Assertion(A): Orthogonalization is applied to the dimensions in linear regression.
Reason(R): Orthogonalization makes univariate regression possible in each orthogonal dimension separately to produce the coefficients.
a. Both A and R are true, and R is the correct explanation of A.
b. Both A and R are true, but R is not the correct explanation of A.
c. A is true, but R is false.
d. A is false, but R is true.
e. Both A and R are false.
Answer:- a
👇For Week 03 Assignment Answers👇
7. Consider the following statements:
Statement A: In Forward stepwise selection, in each step, that variable is chosen which has the maximum correlation with the residual, then the residual is regressed on that variable, and it is added to the predictor.
Statement B: In Forward stagewise selection, the variables are added one by one to the previously selected variables to produce the best fit till then
a. Both the statements are True.
b. Statement A is True, and Statement B is False
c. Statement A if False and Statement B is True
d. Both the statements are False.
Answer:- d
8. The linear regression model y=a0+a1x1+a2x2+…+apxp is to be fitted to a set of N training data points having p attributes each. Let X be N×(p+1) vectors of input values (augmented by 1‘s), Y be N×1 vector of target values, and θ be (p+1)×1 vector of parameter values (a0,a1,a2,…,ap). If the sum squared error is minimized for obtaining the optimal regression model, which of the following equation holds?
Answer:- d
For More NPTEL Answers:- CLICK HERE
Join Our Telegram:- CLICK HERE
| Introduction to Machine Learning | Answers |
| Assignment 1 | Click Here |
| Assignment 2 | Click Here |
| Assignment 3 | Click Here |
| Assignment 4 | Click Here |
| Assignment 5 | Click Here |
| Assignment 6 | Click Here |
| Assignment 7 | Click Here |
| Assignment 8 | Click Here |
| Assignment 9 | Click Here |
| Assignment 10 | Click Here |
| Assignment 11 | NA |
| Assignment 12 | NA |
About Introduction to Machine Learning
With the increased availability of data from varied sources there has been increasing attention paid to the various data driven disciplines such as analytics and machine learning. In this course we intend to introduce some of the basic concepts of machine learning from a mathematically well motivated perspective. We will cover the different learning paradigms and some of the more popular algorithms and architectures used in each of these paradigms.
COURSE LAYOUT
- Week 0: Probability Theory, Linear Algebra, Convex Optimization – (Recap)
- Week 1: Introduction: Statistical Decision Theory – Regression, Classification, Bias Variance
- Week 2: Linear Regression, Multivariate Regression, Subset Selection, Shrinkage Methods, Principal Component Regression, Partial Least squares
- Week 3: Linear Classification, Logistic Regression, Linear Discriminant Analysis
- Week 4: Perceptron, Support Vector Machines
- Week 5: Neural Networks – Introduction, Early Models, Perceptron Learning, Backpropagation, Initialization, Training & Validation, Parameter Estimation – MLE, MAP, Bayesian Estimation
- Week 6: Decision Trees, Regression Trees, Stopping Criterion & Pruning loss functions, Categorical Attributes, Multiway Splits, Missing Values, Decision Trees – Instability Evaluation Measures
- Week 7: Bootstrapping & Cross Validation, Class Evaluation Measures, ROC curve, MDL, Ensemble Methods – Bagging, Committee Machines and Stacking, Boosting
- Week 8: Gradient Boosting, Random Forests, Multi-class Classification, Naive Bayes, Bayesian Networks
- Week 9: Undirected Graphical Models, HMM, Variable Elimination, Belief Propagation
- Week 10: Partitional Clustering, Hierarchical Clustering, Birch Algorithm, CURE Algorithm, Density-based Clustering
- Week 11: Gaussian Mixture Models, Expectation Maximization
- Week 12: Learning Theory, Introduction to Reinforcement Learning, Optional videos (RL framework, TD learning, Solution Methods, Applications)
CRITERIA TO GET A CERTIFICATE
Average assignment score = 25% of average of best 8 assignments out of the total 12 assignments given in the course.
Exam score = 75% of the proctored certification exam score out of 100
Final score = Average assignment score + Exam score
YOU WILL BE ELIGIBLE FOR A CERTIFICATE ONLY IF AVERAGE ASSIGNMENT SCORE >=10/25 AND EXAM SCORE >= 30/75. If one of the 2 criteria is not met, you will not get the certificate even if the Final score >= 40/100.

please provide assignment answers